Examentraining 2

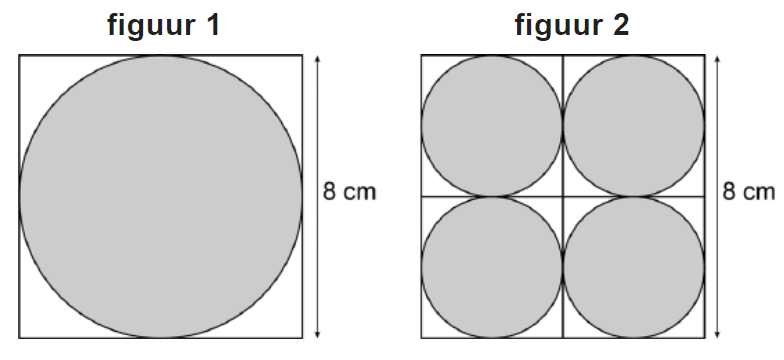
In twee vierkanten met zijden van 8 cm zijn cirkels getekend. In het vierkant van figuur 1 is één cirkel getekend. Bij figuur 2 zijn vier even grote cirkels getekend. Laat in je schrift met een berekening zien dat de oppervlakte van de cirkel van figuur 1 even groot is als de oppervlakte van de vier cirkels samen van figuur 2. Hoe groot is deze oppervlakte? Rond af op 2 decimalen.

Je ziet vierkant ABCD met zijden van 16 cm. In dit vierkant zijn vier vierkanten getekend met elk zijden van 8 cm. In vierkant ABCD zijn vijf cirkels getekend (zie tekening). De middelste cirkel heeft punt M als middelpunt. Bereken, zonder te meten, hoeveel cm de straal van de middelste cirkel is. Schrijf eerst je berekening op en rond je antwoord af op één decimaal.

De regenton van Sven zit vol met water. Vanaf het moment dat Sven het kraantje aan de onderkant van de regenton opendraait, loopt het water eruit. Ga ervan uit dat de hoogte van het water in de regenton daalt. De formule hiervoor staat hieronder. In de formule is h de hoogte van het water in de regenton in meter en t de tijd in minuten met t = 0 op het moment dat Sven het kraantje opendraait. Bereken de hoogte van het water in de regenton in meter op het moment dat Sven het kraantje opendraait (rond af op 2 decimalen). Schrijf eerst je berekening op.

In de formule hieronder is h de hoogte van het water in de regenton in meter en t de tijd in minuten met t = 0 op het moment dat Sven het kraantje opendraait. 

De hoogte van het water in een volle regenton is 1,30 meter. Ga ervan uit dat de regenton cilindervormig is, met een straal van 2 dm. Sven wil een gieter met een inhoud van 14 liter vullen. Hij zet de gieter onder het kraantje van de volle regenton en draait het kraantje open en na precies een halve minuut weer dicht. Hoeveel liter zit er na die halve minuut in de gieter? Rond af op helen. Schrijf eerst je berekening op.

In de formule hieronder is h de hoogte van het water in de regenton in meter en t de tijd in minuten met t = 0 op het moment dat Sven het kraantje opendraait.

Een paar dagen later zit de regenton weer vol met water. Sven zet het kraantje om 13.00 uur open. Bereken hoe laat de regenton volgens de formule helemaal leeg is. Schrijf eerst je berekening op. Geef je antwoord hieronder in de vorm uu.mm (dus bijvoorbeeld 15.20)

Hieronder zie je de voorgevel van het huis. De voorgevel BCFJE is van glas gemaakt. Bereken hoeveel m² de oppervlakte van de voorgevel BCFJE is. Schrijf eerst je berekening op.

We zien weer de voorgevel van het huis.

Bereken hoeveel graden hoek J in de voorgevel BCFJE is. Schrijf eerst je berekening op.

Tijdens de bouw van het huis werden voor de stevigheid de punten B en H en de punten A en J met kabels aan elkaar verbonden. Bereken hoeveel meter de lengte van B naar H is. Schrijf eerst je berekening op.