Quizalize logo
placeholder image to represent content

Q3-M4-L1: Proving Two Triangles are Congruent by (SSS, SAS and ASA)

Quiz by JOCELYN O. HULIP

Grade 8
Mathematics
Philippines Curriculum: Grades K-10 (MELC)

Feel free to use or edit a copy

includes Teacher and Student dashboards

Track each student's skills and progress in your Mastery dashboards

With a free account, teachers can
  • edit the questions
  • save a copy for later
  • start a class game
  • automatically assign follow-up activities based on students’ scores
  • assign as homework
  • share a link with colleagues
  • print as a bubble sheet

Our brand new solo games combine with your quiz, on the same screen

Correct quiz answers unlock more play!

New Quizalize solo game modes
5 questions
Show answers
  • Q1

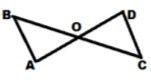
    Congruence postulate will prove that ∆AOB≅∆DOC, If̅ 𝐴𝐵̅̅̅≅ 𝐷𝐶̅̅̅̅ and O is the midpoint of 𝐴𝐷̅̅̅̅ and 𝐵𝐶̅̅̅̅?

    Question Image

    SAA - Th

    ASA - CP

    SSS - CP

    SAS - CP

    30s
    M8GE-IIIg-1
  • Q2

    What are the 2 pairs of corresponding congruent parts that will complete the congruence postulate in the given figure, to prove that ∆AOB≅∆DOC, If̅𝐴𝐵̅̅̅≅ 𝐷𝐶̅̅̅̅ and O is the midpoint of 𝐴𝐷̅̅̅̅ and 𝐵𝐶̅̅̅̅?

    Question Image

    ∠AOB≅ ∠DOC

    AO ≅ OD; OB ≅ OC

    ∠A≅∠D; ∠B≅∠C

    AO≅DO; AB≅ DC

    30s
    M8GE-IIIg-1
  • Q3

    In the accompanying diagram of ∆ABO and ∆CDO, ∠B ≅∠D and AB ≅ CD, which statement is needed to prove Δ ABO ≅ Δ CDO by ASA?

    Question Image

    ∠AOB ≅ ∠DOC

    ∠A ≅ ∠C

    ∠A ≅ ∠D

    ∠C ≅ ∠B

    30s
    M8GE-IIIg-1
  • Q4

    Given the figure where ∠B ≅ ∠C and AB ≅DC, what additional pair of corresponding parts must be congruent for Δ ABD ≅ Δ DCA by SAS?

    Question Image

    \overline{\mathrm{AC\ }}\cong\overline{\mathrm{DB}}

    \overline{\mathrm{AD}}\cong\overline{\mathrm{AD}}

    \overline{\mathrm{BC}}\cong\overline{\mathrm{AD}}

    \overline{\mathrm{AC}}\cong\overline{\mathrm{AD}}

    30s
    M8GE-IIIg-1
  • Q5

    Given an equilateral triangle ABC, with X, Y and Z as the midpoints of ̅𝐴𝐵̅̅̅, 𝐵𝐶̅̅̅̅ and𝐴𝐶̅̅̅̅ respectively. Connecting the midpoints X, Y and Z will result four smaller triangles which are congruent to each other. What congruence postulate will prove that the four smaller triangles are congruent to each other?

    SAA - CTh

    SSS - CP

    ASA - CP

    SAS - CP

    30s
    M8GE-IIIg-1

Teachers give this quiz to your class